Slavic Science meets Bitcoin mining - SHA-256 hashing in the Balkans

No electricity needed. Just a pencil, one piece of paper and a toothpick. Cardboard box optional

Note: this post was heavily influenced by Ken Shirrif’s now 10-year old idea of mining Bitcoin with pencil & paper, here implemented as an exploration of a concept of 256-bit binary number visualizations I’ve been developing in the last 5+ years. The system is called “hash spirals” (or “hash discs” in the previous versions) and you can check different iterations of the system on some of my social profiles.

- Mom can we buy an ASIC card to mine Bitcoin?

- No, we have ASIC card at home

- ASIC card at home:

Using inventiveness akin to Slavic science, a cryptographic algorithm called SHA-256 can now be performed by simply remembering the "rules" of iterating through a compact spiral 2D structure storing binary data (i.e. a piece of paper), as demonstrated in the attached video below.

Prototype of a future mechanical device?

For this first prototype it is done with pencil and a single piece of paper (sustainable af), but it can be turned into a mechanical machine, for example by using wires and abacus-like beads that are painted white on one side and black on the other - indicating 1s and 0s, values of which could be then changed by rotating the beads on the wire. And installing a pointer or clock hand that adjusts with the rotations to show the current dot to look at.

I suppose one of those old telephone mechanisms could also be employed to return the “dial” back to the current segment after the user has finished with each of the 2 XOR rotations. Even though the duct-tape rotation handles are elite level engineering, at least here in the Balkans.

This would work so well here. Or maybe I’m just nostalgic for the 90s.

Or maybe some mechanical engineer wiz reader will have some better ideas, suggestions welcome. In either case, a mechanical version would most likely improve the hashing speed by a significant factor.

Is that a drunken pizza?

Yes.

A cryptographic one. This “hash spiral” system of storing information is explained with images below, if you’re bored with technical details skip this chapter you beta nerd.

There are 16 segments or “slices” of the pizza that go around the spiral in a clockwise fashion. Each slice has the same structure of 24 bits:

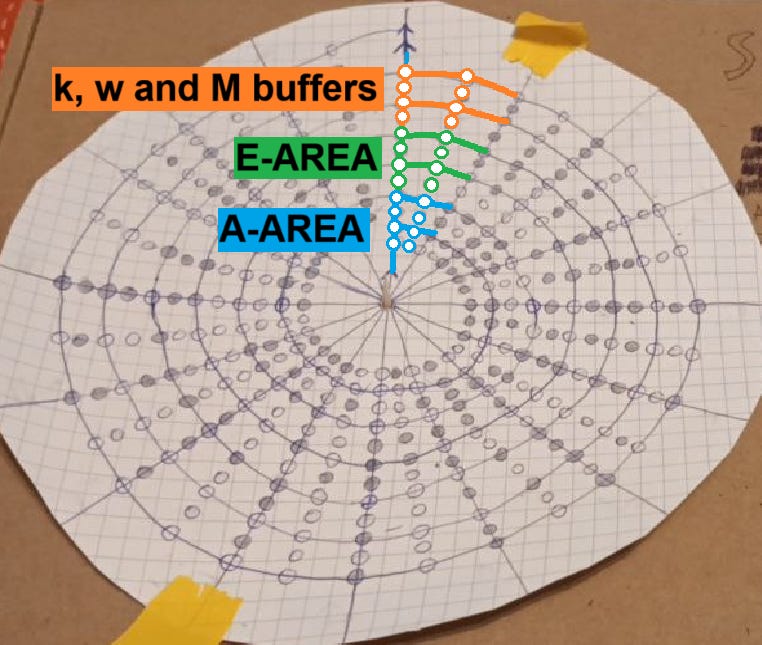
Each segment can be thought of as having 3 distinct areas, this is important to keep in mind for navigating through the spiral while doing rotations:

Each of these areas and the bits within them correspond to relevant parts of the hashing algorithm:

And each of the areas has an upper and lower part, or as I refer to it in the video: an “1st floor” or lower floor and a “2nd floor” or upper floor. These correspond to the first and second parts of the 32-bit binary string of each constant, respectively.

By looking at each segment through these areas, it’s easier to remember the position of bits for each constant in any segment we’re looking at.

For example in the A-Area we have A, B, C and D bits going in a clockwise fashion for each “floor”:

Similarly for the E-Area:

Then at the and, we have the last area which is for the constant k, the input W, and the memory buffers M1 and M2 where we keep track of the different sums and remainders:

So to zoom out a bit, each constant has its bits laid around the spiral in the exact same positions for 2 full circles.

In the example of A, the bits in the 1st floor of A complete 1 circle of the spiral corresponds to the first 16 bits of A:

And the bits in the 2nd floor of A in the 2nd circle of the spiral correspond to the last 16 bits of A, which together with the 1st floor equals to 32 bits in total or the full length of A:

I’ve marked the ending of A on the image above with a short yellow line after the last bit, which indicates that the next bit in the next segment on the same position will be the start of another constant - in this case the constant E. Readers with eagle eye vision will notice there’s another marker like that above it for the end of constant E, as well.

All the other constants and variables can be written and read in the same way by simply going through each segment in the spiral for 2 full circles.

As for the SHA-256 hashing, this modification of the algorithm is simply taking the advantage of the fact that the binary string are laid out in a spiral so by simply “changing the floor” while at a certain position, the miner is essentially skipping 16 bits ahead. I.e. instead of rotating a binary string to the right »6, right »11 and then to the left »25, we do the rotation of clockwise »6, clockwise »5 and then counter-clockwise «2. As long as you remember that you can’t continue from E area into the A area and vice versa, while doing the rotations.

The remainders are stored in the extra positions M1 and M2, while the final shifting of G to H et cetera corresponds to the fact that after the hashing the values stored in G are actually the new values for H, and so on.

The only exceptions being:

• H, which is not used after calculating the first sum in each segment, so it’s just overwritten by D

• D (or “new E” after hashing) which is stored in the D position along with the remainders (since its values are not used for anything else but calculating the new E)

• M1, used to temporarily store the first sum and its remainders for each segment

• M2, which stores the new A value along with the remainders in the same way as the D position stores the new E value

Everything else is without modification as per the SHA-256 hashing algorithm and which is explained in better detail in the already mentioned blog post Mining Bitcoin with pencil & paper.

A hash, or two, per work-week

In this current prototype paper version, one round of the algorithm takes about 45-60 minutes (for beginner-level user) or a hash rate of about 1-2 hashes per every 5 days. Slow, I know. Such is life in the Balkans.

Example of a mined valid block

Here’s how an already mined block would look like (using the same real block example as in Ken’s original blog post, block #286819):

A mined block will have all zeros in the last part of the string, which can be clearly seen by noticing the empty spaces in the positions of G & H constants, highlighted in the image above. Note that last part of F also has some zeroes at the end, which amounts to the difficulty level of that block.

A few interesting things to note:

• AKKCCHHUALLLYYY - yes, I’m aware this algorithm is obviously not comparable to the efficiency of a real ASIC card and/or any computer code running a mining node or just looping through SHA-256 function calls

• along with completing the remaining 63 rounds of the SHA-256 hashing, there are additional steps of manipulating the resulting hash as mentioned previously

• it’s pretty cool that by using this algorithm that’s adjusted for visually interacting with the binary string (instead of algebraically), the binary string gets cut up into slices (indeed like a pizza) and you can quickly notice some interesting things about parts of the resulting hash even during the process

• connected to the previous point, after doing at least a dozen rounds of hashing while developing this approach (and for the purpose of recording the video), one gets accustomed to the flow and it becomes almost second nature, increasing efficiency

• another side-effect of operating this Balkan hashing machine is raised levels of chill - sure as hell beats Sudoku for me, but then again I’m special

• I would even dare to say that at some point in the hashing process there was a sort of weird intuition for what is happening with the information during the hashing process as the areas of full and empty dots move across the board. Not in terms of how close the resulting hash will be to hitting the difficulty condition - because that’s really reaching for it - but definitely a certain acquired taste while visually performing this jumbling-of-bits process that as you’re reading this is being done about 800 quintillion times per second, and that’s usually observed mainly through the lens of computer science, maths and numbers.

Thanks, fellow nerds

If you overly appreciate this nerdgasm here's my addy, I owe some people money: bc1q7xehe7e707ldf9fgrn3648rj5ap5nsud050yr3

P.S. thank you once again to Ken Shirrif for making the video that served both as base inspiration and technical guidance for this post 🙏

---